My violin octet, which you can hear at soundcloud.com/ottotelic/violin-octet, represents a significant part of my ongoing exploration of just intonation. I wrote the 111-minute piece in July 2012, and recorded all 8 parts that fall in the Bushwick studio of my friend Christopher Botta, mixing it with him over the next 9 months. While I hope that the piece offers a meaningful experience to the listener on its own, I would like to give some context for it and explain some of the abstract principles behind it in order to illuminate what it means to me and add another dimension to the listener's experience of the work.
The pitch language of my violin octet is a form of just intonation (JI). While JI is only one of the ways that I deal with pitch as a performer, it has been the primary one for me as a composer for the last several years, and I have found it extremely rewarding and creatively stimulating in both capacities. For me its significance lies in the way it connects the abstract with the sensual, the universal with the particular, the eternal with the transient. As a tool, JI has served different functions for composers of widely divergent aesthetics, and my own understanding and use of JI has changed over time.
I first encountered JI when I was 15 or 16, through the work of Ben Johnston. Johnston had taught at the University of Illinois in Urbana-Champaign, where I grew up, and a former student of his introduced me to the central concept of just intonation, the idea that pitch can be organized rationally, that is, in terms of ratios of frequencies. He drew a diagram of the C major scale in an arrangement I had never seen before, a lattice:
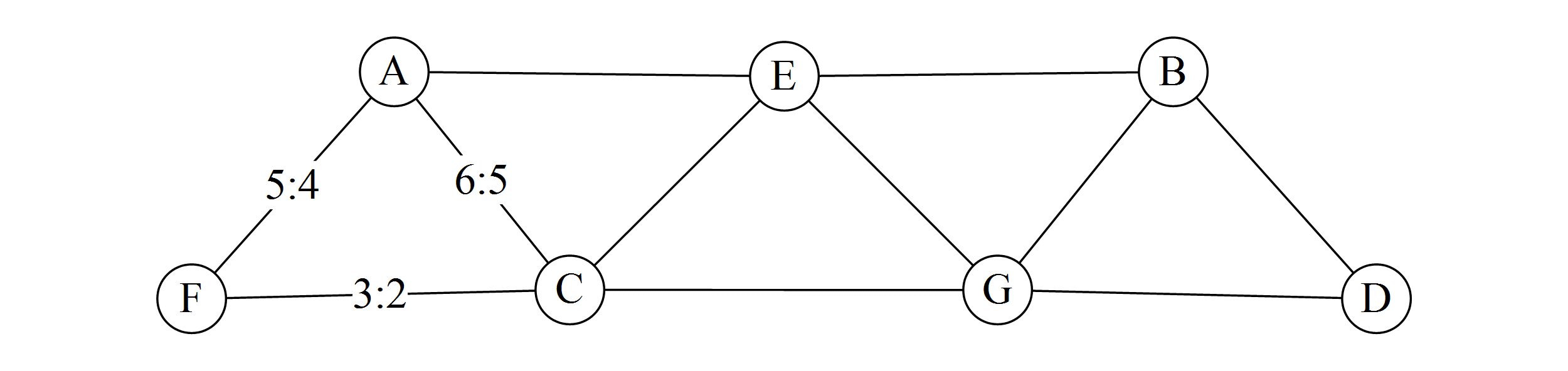
In this orientation, moving one unit to the right on the lattice means going up a perfect fifth, which, he explained, is equivalent to a 3:2 ratio of the frequencies. Going diagonally up and right one unit means ascending a pure major third, 5:4, and moving down and right one unit means ascending a pure minor third, 6:5. The F major, C major, and G major triads form three upward-pointing triangles, which represent frequencies in a 4:5:6 proportion, while the A minor and E minor triads form two downward-pointing triangles, representing the inverse 4:5:6 proportion.
The D minor triad, however, poses a challenge to this system. The existing D and A are not 3:2 apart, but 40:27, so a new pitch, called D- in Johnston's notation, would have to be introduced to the left of A to create another pure minor triad. The difference between this D- and D is a syntonic comma, a ratio of 80:81, or approximately 21.5 cents.
After seeing this lattice I realized that the syntonic comma was the same discrepancy I had heard several years earlier as a violinist playing Kreisler's Preludium and Allegro. I had noticed that if I tuned a B against my D string, it was lower than a B tuned with my E string, but I had no explanation for what I was hearing until I encountered this lattice.
I was beginning to realize that my theoretical conception of pitch and what I was actually hearing were somewhat divergent. JI helped explain the divergence, but it was some time before I realized the new conception of pitch it offered. At that point I had studied traditional music theory, and since starting on the piano at age 5 I had more or less thought that there were simply 12 equal semitones per octave. At the same time, as a violin student, I worked on intonation in part by holding double-stops without vibrato, and since any beating between the harmonics is very apparent in this case, I naturally adjusted the intervals to slow down the beating, which has the effect of pulling the intervals toward just intonation.
Most of the music I was playing at the time was with piano or in an orchestra, where tuning was generally based on equal temperament, and these discrepancies could often be swept under the rug in fast music or when playing with vibrato. However, as I started playing solo Bach and chamber music with other string players, particularly at Eastman, these tuning problems became more exposed in certain situations, and it was (and still is) helpful to know the mathematical logic behind them. I also explored temperaments, which are systems of adjusting pure intervals so that some of these discrepancies disappear.
As a composer, it took some time for me to incorporate just intonation into my music. I loved math and was interested in the mathematical side of music, but since the 12-tone universe was the paradigm I knew best, I initially explored serial music, particularly Babbitt and Schoenberg. I had a friend throughout high school whose father was a composer who had studied with Babbitt, and through him I was introduced the rich and varied connections between math and music within the 12-tone equal-tempered system. I also explored Xenakis's applications of math to composition, which exposed me to radically different possibilities of structuring sound.
From the end of high school to almost the end of my time at Eastman, I used mathematical structures regularly in my compositions. The structures became increasingly abstract in an attempt to create a deep network of meanings. What I lacked, however, was a connection between the abstract relationships I was imagining and how they sounded as music. I would spend many months devising compositional structures that I could understand intellectually, but I was often disappointed when I heard the finished pieces performed. My performing and composing sides diverged, as I was performing a lot of very exciting new and old music at Eastman, but relatively few of my own compositions.
I started bringing my ears into the compositional process in a more direct way with electronic music. I could hear the sonic result of a compositional structure much more quickly and use my perception of it to shape further iterations. I began to create slowly changing drones with sine tones that explored acoustic phenomena resulting from beating and attempted to bridge the timescales of pitch and rhythm.
At the same time, I began working on JI more seriously as a violinist. At UCSD I learned a lot from cellist Charles Curtis, whose mastery of the music of La Monte Young gave me a new appreciation for the amount of time and discipline it takes to develop and explore intonation. In particular, this was the first time I really considered the process of training myself to tune intervals by ear. I soon found that even the simplest task – tuning a single pitch in unison with a sine tone – was an enormously complex and rewarding experience.
The essence of tuning is slowing down beating. Any two frequencies will produce a third frequency equal to their difference, called a difference tone. The closer the pitches, the lower the difference tone, and when it is too low to be perceived as pitch, it becomes a rhythm, which is called beating. Beating can be described as a rhythmic fluctuation of a sound, but what parameter is fluctuating depends on the speed of the beating and the spatial position of the two tones. Faster beating and beating where the tones are not spatially separated produce rhythmic amplitude changes, while slower and more spatially separated beating produce perceptions of timbral fluctuations and rotations in space around the listener.
In the case of tuning a note on the violin to a sine tone, the task is very clear – out of all the sounds present, focusing on and slowing down the beating created between the fundamental of the violin tone and the sine tone. In attempting this task, I began to experience a kind of fusion of the mental and physical, listening with my mind and body. As I focused on slowing down the beating, I became aware of all the precisely coordinated physical adjustments I was making, for example adjusting the left hand finger position microscopically to counteract changes in bow pressure. The beating would slow down to the point where it became an irregular folding and unfolding of the sound, ebbing and flowing. At a certain point the mind – its perception of the sound and the physical sensations of playing – became indistinguishable from the sound itself.
I would also practice with a complex tone such as a sawtooth wave. For a unison, this meant slowing down the overall beating – since each harmonic of the violin note would be beating with the corresponding harmonic of the sawtooth, the task became more ambiguous and subjective. The harmonics of a violin note typically get sharper as they get higher. At a certain point, in order to slow down one beating, another would have to speed up, so I would focus my attention on the sound as a whole and slow down whatever beating was most prominent, a combination of its speed and loudness.
For intervals other than the unison, the beating to slow down would be the harmonics common to both series, the lowest of which I call the reinforced harmonic, which is the least common multiple (LCM) of the two pitches. For example, with a perfect fifth, a 2:3 ratio, the reinforced harmonic would be 6, as the 3rd harmonic of the 2 beats against the 2nd harmonic of the 3.
Practicing intervals as double stops adds the additional challenge of stabilizing two notes at once. I worked on a repertoire of double stops with one open string and one stopped note, starting with the simpler intervals and progressing to more complex ones (e.g., 2:3, 3:4, 3:5, 4:5, 5:6, 4:7, 5:7, 6:7, 5:8, 7:8, 4:9, 5:9, 7:9, 8:9, etc).
Through this process I began to explore the distinctive character and quality of each interval. As the intervals become more complex, the reinforced harmonics become higher and higher, and the difference tones between the notes and their harmonics are particularly useful in defining the intervals aurally. The difference tones between the numerous pairs of harmonics of the notes tend to reinforce each other and grow louder as the interval's intonation stabilizes, and have the effect of filling out the dyad into an entire chord, pointing toward their common fundamental, which is the greatest common divisor (GCD) of the two frequencies.
For example, a 5:7 interval, the simplest just tuning of the tritone, creates this unique pattern of harmonics and difference tones:
| 5 | 7 | difference |
|---|---|---|
| 5 | ||
| 2 | ||
| 7 | ||
| 3 | ||
| 10 | ||
| 4 | ||
| 14 | ||
| 1 | ||
| 15 | ||
| 5 | ||
| 20 | ||
| 1 | ||
| 21 | ||
| 4 | ||
| 25 | ||
| 3 | ||
| 28 | ||
| 2 | ||
| 30 | ||
| 5 | ||
| 35 | 35 | |
| 5 | ||
| 40 | ||
| 2 | ||
| 42 | ||
| etc | etc |
While building up this repertoire of dyads, I started exploring the different ways these dyads could be combined. If the implied fundamentals of two dyads are the same, they have the effect of filling out and strengthening that fundamental. If they are different, but related by a just interval, then they imply an overall fundamental lower than at least one of the dyad's fundamentals. In general, the lower the implied fundamental, the more dissonant the chord, at least in my conception of consonance and dissonance.
I became particularly interested in sets of frequencies in which subsets would be in relatively consonant relationships, but taken together would reinforce a lower, more dissonant fundamental through difference tones or beating. For example, in a constellation of frequencies with proportions 24:25:35:36, the 24:36 reduces to 2:3, and the 25:35 reduces to 5:7, while the 24:25 and 35:36 create difference tones of 1, reinforcing the overall fundamental. These ratios with a numerator and denominator separated by 1 are called superparticular.
In my violin duo, written for and recorded by Erik Carlson, I experimented with ways of linking these types of tetrachords together to create a dynamic melodic/harmonic flow, and my violin octet expands these harmonies both vertically and horizontally to create a sound object that can be heard on many different levels, and to allow ample time for the ear to focus on different aspects of the sound.
In my violin octet, the open strings of violins 1, 2, 5, and 6 are tuned to the 4th, 6th, 9th, and 13th harmonics of a 42 Hz fundamental, while the open strings of violins 3, 4, 7, and 8 are tuned to the 5th, 7th, 11th, and 15th harmonics. Using the intervals I could tune by ear above and below each open string, I generated over a hundred pitches. Calculating the difference tones between each pair of these pitches, I picked the most frequently occurring ones, which form the basis of the first nine sections of the piece. Each of these sections has its own sectional fundamental, which is 42 Hz multiplied by the following ratios: 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 2/15, and 1/10, yielding 42 Hz, 21 Hz, 14 Hz, 10.5 Hz, 8.4 Hz, 7 Hz, 6 Hz, 5.6 Hz, and 4.2 Hz.
For each section, I selected from the complete set of pitches those that are integer multiples (harmonics) of the sectional fundamental. From this list of harmonics, I constructed a chord with at most one dyad in each of the 8 violin parts that would maximize the number of superparticular ratios. These superparticular ratios reinforce the sectional fundamentals because they each create a difference tone of 1.
The chart below shows the collection of harmonics in each section relative to the sectional fundamental shown at the bottom. The absolute frequencies of the first section (which is the complete set of open strings) are shown at the left, and following each open string in a straight line to the right reveals how it functions as a progressively higher harmonic of the progressively lower fundamentals. The superparticular ratios are boxed, and we can notice how a ratio such as 24:25 in the second section recurs in later sections at lower pitch levels. For me each superparticular ratio has a unique flavor due to its unique set of prime factors, but as it is transposed lower it takes on different qualities due to the different beating speeds it creates. At the same time, within a section, the various superparticular ratios with their unique flavors are unified by their identical beating speeds.

These verticalities are also shown in the Extended Helmholtz-Ellis JI notation, treating the 42 Hz fundamental as an E (A=448 Hz). (This notation indicates 5th-harmonic deviations with arrows attached to the accidental, 7th harmonic with a hook, 11th harmonic with a quarter-sharp symbol, and 13th harmonic with a backward flat with an extra vertical line. More information on this notation created by Marc Sabat and Wolfgang von Schweinitz can be found on their website, plainsound.org. This notation and the work of Marc and Wolfgang has been enormously influential and helpful to me, and I recommend exploring their website to learn more about JI.)

Within the pitch collection for a section, the full chord is heard as well as various subsets which illuminate different internal relationships. Some subsets highlight the overall fundamental by emphasizing the superparticular ratios, while other subsets reveal higher fundamentals which are multiples of the sectional fundamental. For example, in section 2, which has the overall fundamental of 21 Hz, the harmonics 9, 12, 18, 24, 27, and 30 share a factor of 3, so when heard in isolation they become harmonics 3, 4, 6, 8, 9, 10 of a fundamental of 63 Hz.
As the piece progresses through the sections, the difference tones go from the realm of pitch to rhythm: from 42 Hz to 4.2 Hz in the first 9 sections, and asymptotically approaching 0 in the final section. Just as each dyad has a characteristic sound and feeling, each of these difference tones has a unique quality. From the opening sonority, the perceived dissonance increases as the fundamentals get lower, but as the beating approaches 0 in the last section, we increasingly perceive the sound as a single entity, a subtly-fluctuating “unison” of harmonics whose fundamental is 252 Hz, the highest fundamental of the piece.
One of my goals in this piece was to create a unified sense of timescale, from the highest audible frequencies to the duration of the entire piece, as a continuum of frequencies/rhythms. The harmonics of the violins occupy the upper end of the frequency range - in particular, the reinforced harmonics of the dyads form a cohesive layer. The fundamentals of the violin notes occupy the mid-range, and the difference tones (and their reinforcement with sine tones at several moments) fill out the lower register and connect to the beating speeds, which occupy the faster rhythmic space (21 Hz to 4.2 Hz) and, in the last section, slow down and approach 0.
The slower rhythmic space is structured by the bow changes. For each dyad, the duration of the downbows and upbows is constant, in part because having a constant bow speed for each double stop helped me to stabilize the intonation and get in a groove. These bow durations (BDs) form a rhythmic counterpoint to the JI pitch relationships, forming polyrhythms and "cascades" which relate to the sectional fundamentals.
The overall tempo of the piece is quarter (“beat”)=63 bpm. I restricted the BDs available in a given section to those that comprise an integral number of cycles of the fundamental for that section. For example, in the first section a 4-beat BD contains 42 cycles/second × 60/63 seconds/beat × 4 beats = 160 cycles of the fundamental of 42 Hz. In theory, this means that the bow changes in all parts would align with the cycles of the fundamental, but as I have not yet been able to control the phase of the beatings so precisely, this is more of a conceptual connection.
Just as a dyad implies a reinforced harmonic and a fundamental, a polyrhythm (in particular one consisting of two constant durations) implies what I call a rhythmic quantum (RQ) and a cycle length. The RQ is the longest duration which subdivides both durations, and equals the GCD of the durations. The cycle length is the minimum duration between alignments of the two rhythms, and equals their LCM.
For example, in the opening section, the four violin parts have BDs of 4 beats, 6 beats, 24/5 beats, and 5 beats. The GCD of these durations is 1/5 of a beat, so the RQ is a quintuplet-sixteenth duration. Since the LCM of these four durations is 120, the four parts align every 120 beats.

This creates a symmetrical structure corresponding to a major/minor triad, with an overall 20:24:25:30 proportion which contains a 4:5:6 (20:25:30) and an inverse 4:5:6 (20:24:30). Because of the symmetry, this 20:24:25:30 structure represents both the number of RQs in each BD and the number of bows in the overall cycle.
In addition to these polyrhythmic structures, there are sections in which multiple parts have the same BD, but are displaced successively at equal durations (the displacement duration, DD). The DD divides the BD evenly, so that the bow duration is subdivided into BD÷DD parts. BD÷DD is often larger than the number of parts present, in which case there is a gap of one or more subdivisions articulated. I think of these composite rhythms as cascades.
For example, immediately after the opening chord (but still within the first section), the 5-beat BD (containing 25 RQs) is adopted by all four parts, with each subsequent part displaced by one quarter note (DD=5 RQs) to create a constant five-beat (25/5=5) cascade of attacks (beat, beat, beat, beat, gap).
In the second section, this five-beat cascade in violins 1, 3, 5, and 7 is pitted against a second, slightly faster cascade in violins 2, 4, 6, and 8. The second cascade has a BD of 24 RQs (the 24/5 beats) and DD of 4 RQs, creating a subdivision into 6 durations: 4 beats plus a 2-beat gap.
Each of the pairs of violins 1 and 2, 3 and 4, 5 and 6, and 7 and 8 create a 24:25 polyrhythm, but start at different points within the overall cycle. Taken together, the two cascades produce a 4:5 polyrhythm (with gaps) at a smaller scale.

In this case, the division of the 8 violins into 2 cascades of 4 violins each mirrors the division of the chord into harmonics of the sectional fundamental that are divisible by 3 and those that are not. Over the course of the piece, the partitioning of the 8 violins into subsets varies, and I use different combinations of polyrhythms and cascades to delineate and connect the subsets.
These rhythmic relationships can be heard on multiple levels - one can listen to the overall composite rhythm, which has the fastest speed of articulation and also the longest cycle, as well as the shorter and slower rhythmic cycles created by various subsets.
For me, the process of recording and mixing the violin octet is as much a part of the piece as the composition on paper. I composed an earlier version of the piece in early 2012 while living in Bushwick, Brooklyn and recorded it over several all-night sessions in the nearby studio of my friend Christopher Botta soon after. A few months later, I realized I was missing an important conceptual link in the material, and recomposed the piece, recording the new version that fall in the same studio while living in Montclair, NJ.
These all-night recording sessions constituted a very intense training in attention. I listened to sine tone versions in headphones to help stabilize the interval. Tuning thus became a multifaceted endeavor – attempting to 1) slow down the beating of each fundamental to the corresponding sine tone, 2) slow down the beating of the reinforced harmonics within the interval, 3) maximize the difference tones, and 4) align my bow changes with the click track. The effect of bow pressure and speed on the intonation of an open string was extremely noticeable – I had to tune open strings at the correct tempo, because if tuning with an arbitrary bow speed I would notice a subtle difference in pitch at the actual tempo.
Attempting to slow down all these beatings while maintaining a steady bow speed engages the mind and body in a subtle and precise relationship. Manifesting the interval as clearly as possible given the physical nature of the instrument, the body, the air, the room, at that moment in time, I was imagining, perceiving, analyzing, hearing, and feeling in myriad ways the presence of a unified entity. For long stretches I felt this entity with my entire being, as different modes of perception became unified, while at the same time I could focus my attention on different aspects of the entity. In playing an interval continuously for many minutes, I could get into a zone where my attention was completely manifest in the sound.
Recording the full duration of each note in complete takes, sometimes lasting ten minutes or more, was important in order to preserve this sense of a continuous evolution of the zone. In layering these zones on top of each other and mixing them with Chris Botta, I aimed to unify them into a still larger entity, encompassing and interrelating the journeys of each note.